Vectors and Muppets, part I

I used to find physicists' naming sense funny. For instance: in 1991, physicists stumbled onto a cosmic particle that was a shocking 20 million times more energetic than anything they had seen before. They creatively called it the "OMG particle". That time they discovered that there is some matter that doesn't interact with light, but still has some gravitational effect on galaxies and stars? "Well, it's matter we can't see, it's... Dark Matter!"

I used to find this funny. But now I work in NLP, and the name of most neural networks we work with are pretty silly themselves. Things were still okay when they were at the level of "We've got something that makes vectors from words? Let's call it word2vec!"

A few years ago came out a paper presenting a new model that turned out to be very popular. The model was technically described as "embeddings from language models", which was shortened to ELMo. A year later, another team came out with a cool concept: bidirectional encoder representations from Transformers. The acronym for that is BERT.

Sesame Street. I kid you not. Anyways. Today's question will be: what are these word2vec and BERT models exactly?

A few posts ago, I briefly explained how you could just compute cooccurrences for some linguistic item, and use that as distributional word vectors. The more dedicated reader will remember that this type of vector was overall unwieldy: a vector with a million or more components is just too much for your computer to handle in a decent amount of time. And that means that, if we want to plug our word vectors as input for our neural networks, then having vectors with fewer components will allow us to have neural models that are faster and simpler to train.

I'll focus on word2vec and BERT, mostly for simplicity. There are a number of different word embedding architectures, many with puns in their names: researchers from Stanford have proposed a model called "GloVe", for instance.

Word2vec is the more ancient of the two: it was proposed by Tomas Mikolov and colleagues in 2013. That model proved to be extremely popular, even outside of NLP: a bunch of studies in linguistics or psychology of language have used some variation thereof. I'll start with word2vec for today, my next post will be on BERT.

The core idea behind word2vec is pretty straightfoward: we'll train a simple model that learns a fairly simple task. Either we train it to predict what word occurs in a given context, or we train to predict what's the likely context of a word. These two variants have names: we call the former a CBOW word2vec model, and the latter a skip-gram word2vec model.

Just to drive the point home, let's go over an example. We'll assume we have some target word, like away and some context of occurrence, such as you'll never get away with this!. In a CBOW model, we'll get to predict away from the context, whereas in a skip-gram model, we'll predict each word in the context using as input the target word away.

But, you may ask, how exactly are we to use words as inputs to numerical models? The means we have to train models, as I described in the previous post, requires that we use numerical inputs. The one trick we use here consists in defining a mapping between words and vectors. We'll start with purely random vectors, and we'll allow the model to also optimize their values. So any time I need to use the word away as input to my model, I'll just swap that for the corresponding vector. Once my model is trained, it will also contain this collection of word vectors.

The technique of Mikolov and colleagues was more efficient than most other neural approaches at the time. They provided an efficient piece of software, which didn't require much more than your average computer to train a model on a large amount of data. What was neat is that the word vectors you would get from a word2vec model could be re-used in more complex models and greatly increase performances.

From a linguistic perspective, we can also point out that the vectors have been trained on a pretty distributional task. It didn't take long for researchers to agree that word2vec vectors were also distributional representations.

What really got the party going was that Mikolov and colleagues also showed that their vectors weren't just randomly distributed in a high dimensional space. The first thing they pointed out was that semantic contrasts tended to be represented by parallel components: since man vs. woman, aunt vs. uncle, or king vs. queen express the same semantic difference, then their corresponding vectors should express the same vector difference. This parallelism entailed that you could do basic vector operation to predict, manipulate and retrieve word vectors, based on what the underlying words meant.

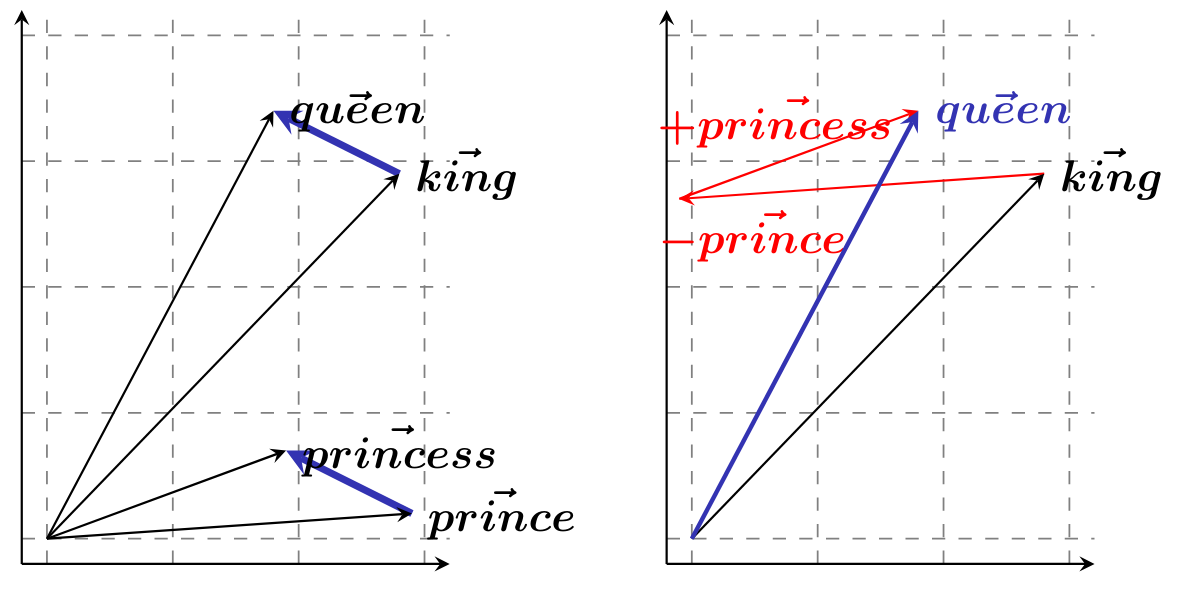
I should note that there has been some criticism of this last remark. First, it's not just semantic differences that can get encoded that way: stereotypes can also end up encoded in the same way. For instance, Bolukbasi et al reported that you could find a parallel structure between man vs. computer programmer and woman vs. homemaker. Second, there is a body of work dedicated to showing that the methodology we use to discover and test these parallel structures is somewhat flawed. It's science. It's complicated.

Anyways, I'll stop here for this week. See you next time!