Your dictionary at a distance

Last time (which admittedly was some time ago) we talked about why I wanted to compare embeddings and definitions. This time I'm going to talk about how to do that.

You got it! It's experiment time! Don't go expecting any death-ray doomsday machine or any explosive chemical mix. An experiment is fundamentally something to produce observations. You do something (e.g., you pour a mysterious liquid X onto a mallard) and you observe the results (said mallard becomes feral and proceeds to attack the lab assistant). It's in that sense that I'm refering to such work as "experiments". Nonetheless, we can also spare a few words to see how an experiment in Computational Linguistics differs from your expectations.

Suppose I am a mad biologist interested in the development of mutant super-ducks. Here, my experiment of pouring mystery liquid X onto a duck will produce an observable results that is a cold, hard fact: either the lab assistant is dead and I'm on my way for an Ignobel prize (or prison), or he's not and I've disproven that mystery liquid X has the properties I believed it to hold.

But most of CL/NLP experiments are going to be modeling work: we come up with some model of how we expect language to be (for instance, that linguistic meaning has something to do with how often words occur together), and then we derive predictions from that model to match against some previously made observations. The only "observation" we make in this case is whether our theory holds water or not—there's few feral waterfowl for us to find confort in.

Even worse, modeling work is a lot harder to disprove that direct experiments. You can always tweak the math, update the parameters and try again to see if now it's working. And then it ends up working, because any sufficiently complex machine will end up matching with any sufficient small set of observations. So we want our models to be super simple: the less we can tweak, the less we can cheat. We also want the datasets we compare ourselves to be large: the more data we accrue, the more likely it is that our model is in fact generalizing properly.

With that in mind, what is the simplest way to compare dictionary definitions and word embeddings? My take here is that both embeddings and definitions have some built-in notion of distance, and we can see if the two match. If the meaning of two words, say "Friday" and "Thursday" are close, then we can expect their embeddings to be close, and their definitions to be similar. On the whole, if embeddings and definitions encode the same thing, we culd expect the distances between definitions to correlate with the corresponding distances between embeddings.

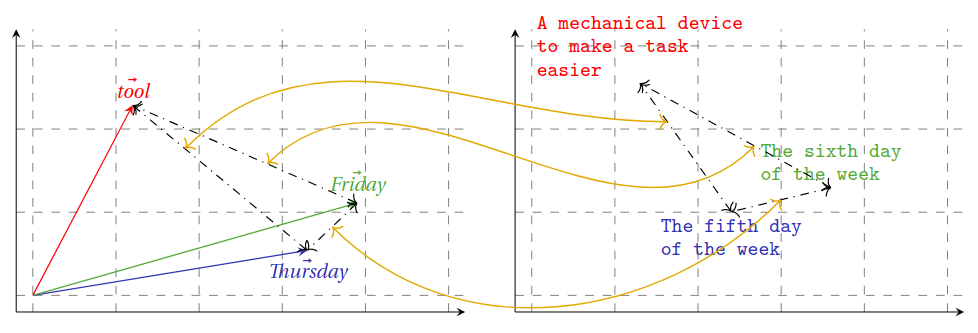
There's many ways to define a distance between definitions. A simple onewould be the edit distance, a.k.a. the Levenshtein distance: we count the minimum number of words you need to add, change or remove to change one definition into another. So to change The fifth day of the week into The sixth day of the week, we'd have to change one word, and that gets us a distance of one. To change The fifth day of the week into A mechanical device to make a task easier, we'd have to have a distance of 8. We could also normalize that so that the maximum is 1 (when you need to change everything), to do that, we only need to divide by the number of words in the longest of the two sentences.

Likewise, we have many ways to set up distances between vectors. We can think of angular distance, which we'd mesure using cosine, or think about Euclidean distance, just like you did all these years ago in geometry class.

Once we have distances between embeddings and definitions sorted out, we can measure how correlated the two are. Here's a snippet of some of the results you'd get from doing that:

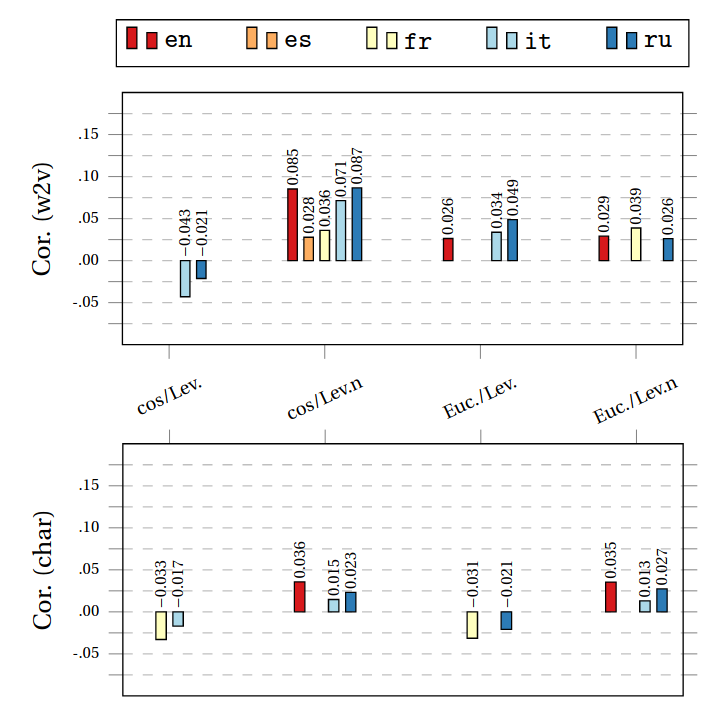
In the picture above, we have data from five languages (English, Spanish, French, Italian and Russian), each with their own matching color. I tested different distances for definitions and embeddings (that's why you have multiple groups of bars). Lastly, the top plot is for distributional embeddings computed using word2vec, whereas the bottom one corresponds to vectors I computed from some other piece of linguistic information (namely spelling). Missing bars correspond to statistically insignificant correlations: measurements that could just as well correspond to random flukes are not displayed.

Concretly, the left-most, top-most redbar labelled 0.085 tells you that the cosine distance between English word2vec embeddings and the normalized Levenshtein distance between English definitions yield a correlation of 0.085.

But what does this bunch of numbers tell us, you ask? I'm glad you asked! I don't really know for sure, or if I had to put it in a more formal academic jargon, I would tell you it's "sort of all over the place, kind of". If we look at the word2vec embeddings, in some cases we find no significant correlations, in other we have anti-correlations (i.e., vectors we judge to be similar tend to get definitions we'd judge to be different). There's no clear trend across languages. Even when we get a correlation, it's low: 0.085, when the maximum possible value would be 1.

It's not all bad, though: it's nice to see that overall, distributional vectors like word2vec tend to have higher correlation scores than spelling-based vectors. It does suggest that whatever word2vec encodes, it's more like definitions than what spelling-vectors encode.

Overall, even when trying to have a simple, straightforward experiment, it's hard to control for everything. So we're in a situation where we don't have a feral duck, but we've been bitten by the damn beast nonetheless. It's not a clear-cut result. Science rarely is clear-cut. But still, I'm not sure this piece of evidence suggests that distributional semantic representations like word2vec vectors have nothing to do with definitions, or if it suggests that the distances I chose were just the wrong ones for this experiment, or that my basic expectation that distances between deifnitions should match distance between vectors was just wrong. If anything, this tells us one thing: the story is more complicated than you might expect at a glance.

There's only one thing left to do. Build a death-ray giant sentient robot. Do more science.