Can a machine write a dictionary?

Last time, we went over a simple experiment design where we wanted to check how the distance between two definition glosses compare to the distance between two embeddings. It turned out poorly. So let's take the road not taken previously: what can we find out about how similar definitions and embeddings are if we just throw everything we have at this problem? Let's bring out the big guns since the peashooter didn't help.

The big guns, so to speak, would be neural networks. You might want to reread the previous blog post on gradient descent (post #8 here), but the basic facts I'd like you to keep in mind is that we're talking huge, complex models with gazillions of dials and knobs to adjust. The immediate consequence to that is that you don't know what every individual knob or dial is doing: we give the model some input and it produces some output that we can judge and optimize.

How do we use these neural networks to answer our problem? How can I massage a neural network to tell me if a word vector is not equivalent to the corresponding definition? What we can do is give the network a definition as an input, and task it with reproducing the corresponding vector as its output. If it fails miserably, then we can consider that the two are not equivalent—since if you can't reconstruct an embedding from a definition, then the definition is lacking some of the information that is encoded in the target embedding. We can also look at the other way round and see whether we can generate the definition from the embedding.

It turns out that these two neural network tasks already exist (more or less) in the NLP literature. Transforming an embedding into the matching definition is known as definition modeling. It's actually a fairly recent to the NLP landscape: the seminal paper by Noraset et al. on the topic dates from one or two years before the start of my thesis.

The converse task does not exist per se, but you can think of it as a reverse dictionary of sort. A reverse dictionary is a plain old dictionary, but reversed: you're looking up a word by thinking up what its definition should be, and looking for that within the document. There are a few use-cases where it might be useful: mostly for solving crosswords and writing prose.

I had the opportunity of framing this experiment as a shared task. A shared task is essentially a competition between scientists: there's a leaderboard and participants are trying to get as high as they can. The shared task I organized was called CODWOE, for "COmparing Dictionaries and WOrd Embeddings", hence the fabulous logo I came up with.

We gave participants access to some dictionary definitions (drawn from wiktionary) and embeddings (that we trained ourselves) and had them try to generate definitions from embeddings and embeddings from definitions. We also ran some fairly simple baselines to give a sense of scale. It was an interesting learning experience; there's a lot I wouldn't do in the same way if I was to redo the whole project again.

And so, you may ask, how well did it go? Well, much like with our previous distance-based experiments, the answer isn't super clearcut. Here's a look at part of what we got:

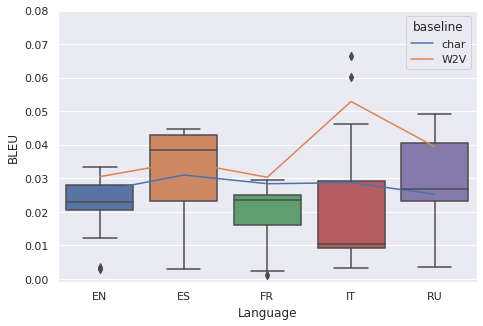
These results are only for definition modeling. Just like in the previous post, you'll find the same five languages we used (English, Spanish, French, Italian and Russian) and the same two types of embeddings (word2vec, "w2v" on the plot and spelling-based, or "char"): the lines correspond to the scores we get for our baseline models, using either spelling vectors or distributional vectors as input. The boxplots for each language are the participants' scores.

Two key remarks. First: we're ranking models sing BLEU scores. BLEU is a metric that, informally speaking, counts the number of tokens and/or sequences of tokens that match in the produced output and the target definition. The minimum value it can get is 0, the best value would be 1; higher is better. Here, what you might not notice is that the scores are extremely low—so low that the scores are roughly on par with nonsensical random strings of tokens.

On the other hand, the other thing to remark is that we do get systematically better results using distributional vectors like word2vec than what we have with spelling vectors. It's hard to make a definitive call, given that we're looking at very low scores.

Let's go a bit deeper into the weeds: can we explain why we got such low scores?

I have two pieces of evidence to provide here. The first is that we actually have a mismatch: a definition corresponds to a word sene, whereas an embedding corresponds to a word type. While I would get two distinct definitions for to duck and a duck, I am only going to get one embedding for the string of characters duck. As a consequence, most (if not all) works in definition modeling include some example of usage, so that the model can learn to disambiguate word senses based on context of usage. In this shared task, we only provided embeddings without any context of usage: this means that the task was more difficult than what the usual definition modeling task.

The second bit of evidence we can discuss is that massive neural networks tend to not be very good at discriminating between different types of embeddings. By that, I mean that there are so many knobs and dials to turn that a network can overcompensate for any defects in your embeddings. That's something we can see if we compare errors across multiple benchmarks for embeddings. For instance, if you recall the word analogy task we discussed a few posts ago (post #9 here), we can see that while not all word vectors yield the same performances on analogy, the type and numbers of errors they make on definition modeling is more or less the same:

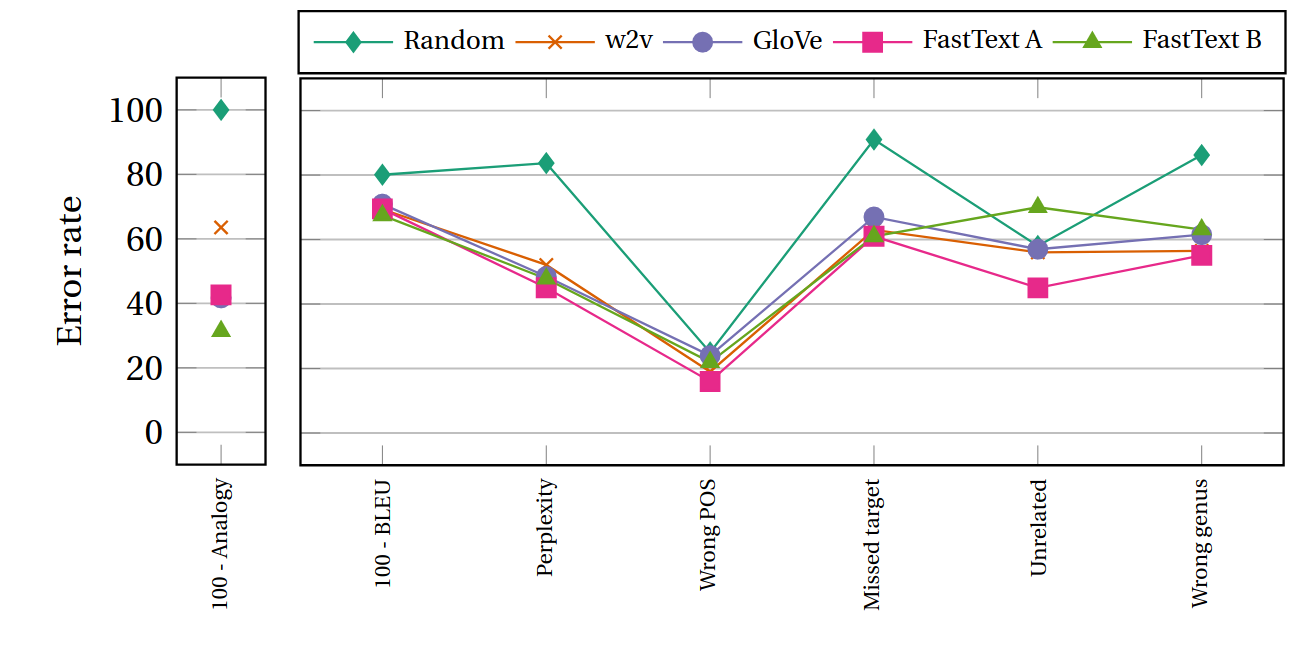
Here, we have a bunch of error metrics for definition modeling: the BLEU score which I discussed earlier, perplexity (how unlikely is it that the model would produce the target definition), plus a bunch of manually annotated errors metrics ranging from the proportions of definitions where the part of speech doesn't match (e.g., where the model defines a duck instead of to duck) to the proportion of definitions where the model is completely off the mark (e.g., defining a researcher as a type of cloth). The plot tracks different vectors: from completely random ones, where I just did the computer science equivalent of rolling a dice to attribute a vector, to our good old word2vec friends.

The crucial point is that the analogy setup only relies on us adding vectors together, whereas the definition modeling metrics are based on a neural network. So if we consider performance on word analogy a reliable indicator of embedding quality, we get to observe how the definition modeling network overcompensates discrepencies in quality.

What we see is that as far as analogy is concerned, the random vectors get the worst possible grade (they get 100% of their answers wrong), whereas the various distributional vectors we have tend to yield different scores. On the other hand, on definition modeling, the random vectors are the only one that are clearly distinguishable, and even then they don't automatically get the worst possible score across the board. As for the distributional vectors, it's basically a toss up. In short, the model overcompensates the quality of the embeddings.

Okay, this post is getting quite long, so let's try to wrap it all up. Can we use neural networks to write definitions using embeddings? In theory, we can set up something, and see how it goes. In practice, the results are fairly disappointing: scores are poor, models are prone to over-compensate, and we also need to tack on examples of usage if we want to get a working system.

In fact, this points towards the basic underlying assumption we've followed thus far being wrong: there's something fundamentally unlike definitions encoded in word embeddings. That's what we'll focus on in the next few blog posts!